Question

Of a group of randomly selected adults, 360 identified themselves as manual laborers, 280 identified themselves as non-manual wage earners, 250 identified themselves as mid-level managers, and 160 identified themselves as executives. In the survey, 295 of manual laborers preferred trucks, 174 of non-manual wage earners preferred trucks, 135 of mid-level managers preferred trucks, and 42 of executives preferred trucks. We are interested in finding the 95% confidence interval for the percent of executives who prefer trucks.

Which distribution should you use for this problem?

Construct a 95% confidence interval.

State the confidence interval and interpret this result in regards to the context of the problem.

Answer 1

We are 95% confident that the percent of executives who prefer trucks is between 19.43% and 33.06%

Explanation:

We are given that in a group of randomly selected adults, 160 identified themselves as executives.

n = 160

Also we are given that 42 of executives preferred trucks.

So the proportion of executives who prefer trucks is given by

p = 42/160

p = 0.2625

We are asked to find the 95% confidence interval for the percent of executives who prefer trucks.

We can use normal distribution for this problem if the following conditions are satisfied.

n×p ≥ 10

160×0.2625 ≥ 10

42 ≥ 10 (satisfied)

n×(1 - p) ≥ 10

160×(1 - 0.2625) ≥ 10

118 ≥ 10 (satisfied)

The required confidence interval is given by

`$ p \pm z* \sqrt{(p(1-p))/(n) } $`

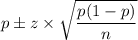
Where p is the proportion of executives who prefer trucks, n is the number of executives and z is the z-score corresponding to the confidence level of 95%.

Form the z-table, the z-score corresponding to the confidence level of 95% is 1.96

`$ p \pm z* \sqrt{(p(1-p))/(n) } $`

`$ 0.2625 \pm 1.96* \sqrt{(0.2625(1-0.2625))/(160) } $`

`$ 0.2625 \pm 1.96* 0.03478 $`

`$ 0.2625 \pm 0.06816 $`

`0.2625 - 0.06816, \: 0.2625 + 0.06816`

`(0.1943, \: 0.3306)`

`(19.43\%, \: 33.06\%)`

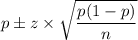
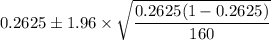
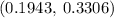
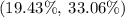
Therefore, we are 95% confident that the percent of executives who prefer trucks is between 19.43% and 33.06%