Question

You are to make four straight-line moves over a flat desert floor, starting at the origin of an xy coordinate system and ending at the xy coordinates (-154 m, 76 m). The x component and y component of your moves are the following, respectively, in meters: (20 and 60), then (bx and -70), then (-20 and cy), then (-60 and -70). What are (a) component bx and (b) component cy

Answer 1

Explanation:

You are to make four straight-line moves over a flat desert floor, starting at the origin of an xy coordinate system and ending at the xy coordinates (-154 m, 76 m). The x component and y component of your moves are the following, respectively, in meters: (20 and 60), then (bx and -70), then (-20 and cy), then (-60 and -70). What are (a) component bx and (b) component cy

(c) What is the the magnitude of the overall displacement?

(d) What is the angle (relative to the positive direction of the x axis)?

1(a) component bx

`20 + b_x - 20 - 60 = -154\\b_x=-154+60\\ b_x = -72m`

b)component cy

`60-70+c_y-70=76\\c_y=76+80\\c_y=156m`

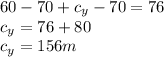
2) Magnitude

we use pythagoras theorem to solve the magnitude of the resultant vector

`|r|=√((-154)^2+(76)^2) \\=√(23716+5776) \\=√(29492) \\=171.73m\approx172m`

lastly we use the following trigonometry to solve for θ

`\theta = \tan (\frac76}{-154} )^(-1)\\=\tan(-0.4935)^(-1)\\=-26.3^0`

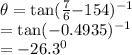
= -26.3° going clockwise from the negative x direction

However, it is in the 2nd quadrant , thus from positive x-direction , it would actually be 152°