Answer:
Amplitude = -3
Period =
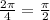
Frequency =
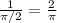
Vertical Shift = 6.
Explanation:
Consider the function:
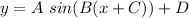
Here,
A = amplitude; It is the measure of how high is the peak from the center line.
2π/B = period; A period is the distance between one peak to the next.
C = phase shift; it represents how far the function is shifted horizontally from the initial point.
D = vertical shift; it represents how far the function is shifted vertically from the initial point.
The frequency of a function is the number of times something happens per unit time.
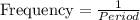
The function provided is:
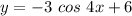
On comparing the provided function with the general one it can be determined that:
Amplitude = -3
Period =
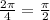
Frequency =
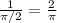
Vertical Shift = 6.