Question

What is the length of a radius of the circle represented by the equation below?

x2 + y2 - 4x – 4y + 4 = 0?

Answer 1

2

Explanation:

Given the circle:
`x^2 + y^2 - 4x - 4y + 4 = 0`

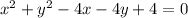
To determine the length of the radius, we complete the square.

Step 1: Subtract 4 from both sides

`x^2 + y^2 - 4x - 4y + 4 -4= 0-4\\x^2 + y^2 - 4x - 4y = -4`

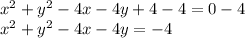
Step 2: Divide the coefficient of x and y by 2, square it and add it to both sides

`x^2 - 4x+(-2)^2+ y^2 - 4y+(-2)^2 = -4+(-2)^2+(-2)^2`

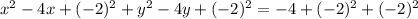
Step 3: Factorize the Left Hand side and simplify the Right Hand side.

`(x-2)^2+ (y-2)^2 = 2^2`

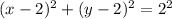
Comparing with the standard form of the equation of a circle

`(x-h)^2+ (y-k)^2 = r^2`

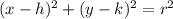
r=2

Therefore, the radius of the circle is 2.