Answer:
a. x = 40 wpm
b. MOE = 4.4 wpm.
c. If you were to create many more confidence intervals from many different random samples, you would expect 95% all of the confidence intervals to have centers and widths that include the true mean.
d. About 5% of the confidence intervals would not capture the parameter (true mean) you are trying to estimate.
Explanation:
We have a 95% confidence interval for the mean with bounds 35.6 and 44.4.
This is estimated from a sample that, in this case, has a sample size of n=54.
The value of x, used to construct the interval, will be at the center of the interval. Then we can calculate the value of x as the average between the two bounds:

The margin of error is equal to the difference between x and any of the bounds:
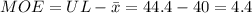
c. If you were to create many more confidence intervals from many different random samples, you would expect 95% all of the confidence intervals to have centers and widths that include the true mean.
d. About 5% of the confidence intervals would not capture the parameter (true mean) you are trying to estimate.