Answer:
Twice as fast
Step-by-step explanation:
Solution:-
- The mass of less massive cart = m
- The mass of Massive cart = 2m
- The velocity of less massive cart = u
- The velocity of massive cart = v
- We will consider the system of two carts to be isolated and there is no external applied force on the system. This conditions validates the conservation of linear momentum to be applied on the isolated system.
- Each cart with its respective velocity are directed at each other. And meet up with head on collision and comes to rest immediately after the collision.
- The conservation of linear momentum states that the momentum of the system before ( P_i ) and after the collision ( P_f ) remains the same.
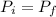
- Since the carts comes to a stop after collision then the linear momentum after the collision ( P_f = 0 ). Therefore, we have:
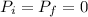
- The linear momentum of a particle ( cart ) is the product of its mass and velocity as follows:
m*u - 2*m*v = 0
Where,
( u ) and ( v ) are opposing velocity vectors in 1-dimension.
- Evaluate the velcoity ( u ) of the less massive cart in terms of the speed ( v ) of more massive cart as follows:
m*u = 2*m*v
u = 2*v
Answer: The velocity of less massive cart must be twice the speed of more massive cart for the system conditions to hold true i.e ( they both come to a stop after collision ).