Question

What is the value of the arithmetic series below?

S19= 19/E/k=1 (4-3k)


a) -494

b) -104

c) -53

d) -52

Answer 1

the answer is A. -494

edge 2021

Explanation:

Answer 2

(A)-494

Explanation:

Given the arithmetic series

`S_(19)=\sum_(k=1)^(19)4-3k`

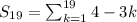
The terms in the sequence are:

• When k=1, 4-3k=4-3(1)=1
• When k=2, 4-3k=4-3(2)=-2
• When k=3, 4-3k=4-3(3)=-5

Therefore, the terms in the sequence are: 1, -2, -5, ...

First term, a =1

Common difference, d=-2-1=-3

The sum of an arithmetic series,
`S_n=(n)/(2)[2a+(n-1)d]`

Therefore:

`S_(19)=(19)/(2)[2(1)+(19-1)(-3)]\\=9.5[2+18*-3]\\=9.5[2-54]\\=9.5*-52\\=-494`

The correct option is A.