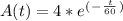Question

A tank contains 300 liters of fluid in which 40 grams of salt is dissolved. Pure water is then pumped into the tank at a rate of 5 L/min; the well-mixed solution is pumped out at the same rate. Let the A(t) be the number of grams of salt in the tank at time t. Find the rate at which the number of grams of salt in the tank is changing at time t. dA dt = Find the number A(t) of grams of salt in the tank at time t. A(t) = g

Answer 1

The rate of change of salt in the tank is given by the differential equation dA/dt = -(5 L/min) * (A(t)/300 L), which after solving, results in the expression A(t) = 40*e^(-t/60) grams. This equation describes the amount of salt in grams at any time t, considering the solution is continuously well-mixed.

Step-by-step explanation:

To find the rate at which the number of grams of salt in the tank is changing, we can set up a differential equation based on the information given. The tank initially contains 300 liters of fluid with 40 grams of salt dissolved in it. For the rate of change of the amount of salt, let A(t) be the number of grams of salt in the tank at time t.

Pure water enters the tank at a rate of 5 L/min and the well-mixed solution leaves at the same rate. This dilution process can be expressed as a first-order differential equation:

dA/dt = -r*(A(t)/V)

Where:

r is the rate at which the water flows in and out (5 L/min).

V is the volume of the tank (300 liters).

Substituting the values, we get:
dA/dt = -(5 L/min) * (A(t)/300 L)

This relationship reflects that the salt is being washed out at a rate proportional to its current concentration. Solving this differential equation gives us A(t), the amount of salt in the tank at any time t:

A(t) = 40*e-t/60 grams

Here, the initial amount of salt is 40 grams, and the factor of 60 in the exponent comes from the ratio of the tank's volume to the rate of water flow (300 L / 5 L/min).

Answer 2

`A(t) = 4*e^(^-^(t)/(60)^)`

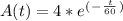
Step-by-step explanation:

Solution:-

- The amount of salt in the solution is ( A ) at any time t.

- Pure water enters the tank ( no salt ( A = 0 ) ).

- The volumetric rate of flow in and out of tank is V(flow) = 5 L / min

- The rate of change of salt in the tank at time ( t ) can be expressed as a first order ordinary differential equation for the salt solution that flows in and out of the tank

- The first order ordinary differential equation is expressed as:

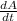`(dA)/(dt)` = ( salt flow in ) - ( salt flow out )

- Fresh water with zero salt content flows in then ( salt flow in ) = 0

- The concentration of salt within the tank changes with time ( t ).

- The volume of water in the tank remains constant ( steady state conditions ). I.e 5 Liters volume leaves and 5 Liters is added; hence, the total volume of solution in tank remains 300 Liters.

- So at any instant the concentration of salt in the 300 Liter tank is:

`conc = (A(t))/(300)*(kg)/(L)`

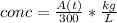
- The amount of salt-solution flowing out of the tank per unit time would be:

`flow-out = conc * V( flow-out )`

`flow-out = (A(t))/(300)(kg)/(L) * 5(L)/(min)`

`flow-out = (A(t))/(60) (kg)/(min)`

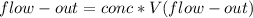
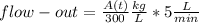
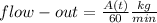
- The differential equation becomes:

`(dA)/(dt) = 0 - (A)/(60)`

- Separate the variables and integrate both sides:

`\int {(1)/(A) } \, dA = - \int {(1)/(60) } \, dt + c \\\\Ln ( A ) = -(t)/(60) + c\\\\A = C*e^(^-^(t)/(60)^)`

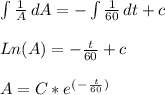
- Initial conditions: A ( 0 ) = 4 grams. Use the initial conditions to evaluate the constant of integration:

`4 = C*e^0 = C`

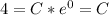
- The solution to the differential equation becomes::

`A(t) = 4*e^(^-^(t)/(60)^)`