Answer:
![[x=(1(4)+3(-2))/(1+3), y=(1(7)+3(4))/(1+3)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/to3ge7trsobmfkc8glhqw10ivyauh5crch.png)
![[x=(4-6)/(4), y=(7+12)/(4)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/po62r0at3340w0h2hvx5qixvb7oexg0vnt.png)
![[x=(-2)/(4), y=(19)/(4)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4j6ks8t2xlf6wi7r6ch9dfjzdoc3ut6efg.png)
![[x=-0.5, y=4.75]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nk73flphhf7zqetvwe3mfg9xmq7twbzvu9.png)
Therefore, the coordinates of point 'b' would be (-0.5 , 4.75).
Explanation:
We have been given that point a is at (-2,4) and point c is at (4,7) .
We are asked to find the coordinates of point b on segment ac such that the ratio is 1:3.
We will use section formula to solve our given problem.
When point P divides a segment internally in the ratio m:n, the coordinates of point P would be:
![[x=(mx_2+nx_1)/(m+n), y=(my_2+ny_1)/(m+n)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/qqgoce6bmwm3v5bq7f9qzrb8arps82dm5b.png)
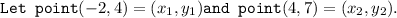
![[x=(1(4)+3(-2))/(1+3), y=(1(7)+3(4))/(1+3)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/to3ge7trsobmfkc8glhqw10ivyauh5crch.png)
![[x=(4-6)/(4), y=(7+12)/(4)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/po62r0at3340w0h2hvx5qixvb7oexg0vnt.png)
![[x=(-2)/(4), y=(19)/(4)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/4j6ks8t2xlf6wi7r6ch9dfjzdoc3ut6efg.png)
![[x=-0.5, y=4.75]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/nk73flphhf7zqetvwe3mfg9xmq7twbzvu9.png)
Therefore, the coordinates of point 'b' would be (-0.5 , 4.75).