Question

Express f(x) = 3 cos x + 5 sin x as Rsin(x + o), where e
is an acute angle in radians.​

Answer 1

√34sin(x + 0.33π)

Explanation:

The general form of the equation acosx + bsinx = Rsin(x + e) where R is the resultant of the constants 'a' and 'b' and e is the angle between them.

R = √a²+b²

`e = tan^(-1)(b)/(a)`

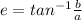
Given the function f(x) = 3 cos x + 5 sin x, comparing with the general equation;

a = 3, b = 5

R = √3²+5²

R = √9+25

R =√34

`e = tan^(-1) (5)/(3) \\e = 59.09^(0)`

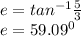
in radians;

`e =(\pi )/(180)*59.09\\ e = 0.33\pi rad`

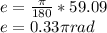
3 cos x + 5 sin x = √34sin(x + 0.33π)