Question

C) Three AC voltages are as follows:

e1 = 80 sin ωt volts;
e2 = 60 sin (ωt + π/2) volts;
e3 = 100 sin (ωt – π/3) volts.
Find the resultant e of these three voltages and express it in the form
Em sin (ωt ± φ). [5 MARKS]
When this resultant voltage is applied to a circuit consisting of a 10-Ω resistor and a capacitance of 17.3 Ω reactance connected in series, find an expression for the instantaneous value of the current flowing, expressed in the same form. [4 MARKS]

Answer 1

E = 132.69 sin(ωt -11.56)

i(t) = 6.64 sin (ωt +48.44) A

Step-by-step explanation:

given data

e1 = 80 sin ωt volts 80 < 0

e2 = 60 sin (ωt + π/2) volts 60 < 90

e3 = 100 sin (ωt – π/3) volts 100 < -60

solution

resultant will be = e2 + e2 + e3

E = 80 < 0 + 60 < 90 + 100 < -60

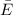`\bar E` = 80 + j60 + 50 - j50
`√(3)`

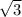
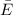`\bar E` = 130 + (-j26.60)

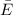`\bar E` = 132.69 that is less than -11.56

so

E = 132.69 sin(ωt -11.56)

and

as we have given the impedance

z = (10-j17.3)Ω

z = 19.982 < -60

and

i(t) =
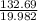`(132.69)/(19.982)` sin(ωt -11.56 + 60)

i(t) = 6.64 sin (ωt +48.44) A