Question

A statistics professor has found that a student who studies 90 minutes each day has a probability of .9 of getting a grade of C or better, while a student who does not regularly study 90 minutes each day has a probability of .2 of getting a C or better. It is known that 70% of the students are following this recommendation. Find the probability that, if a student has earned a C or better, that they have followed the professor's study recommendation (to 3 decimal places).

Answer 1

91.30% probability that they have followed the professor's study recommendation

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

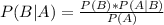
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Student earned a C or better.

Event B: Student followed the professor's study recommendation.

70% of the students are following this recommendation.

This means that
`P(B) = 0.7`

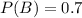
A statistics professor has found that a student who studies 90 minutes each day has a probability of .9 of getting a grade of C or better

This means that
`P(A|B) = 0.9`

Probability of earning C or better.

90% of 70%(those who followed the study recommendations).

20% of 30%(those who did not follow the study recommendations. So

`P(A) = 0.9*0.7 + 0.2*0.3 = 0.69`

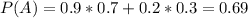
Find the probability that, if a student has earned a C or better, that they have followed the professor's study recommendation:

`P(B|A) = (0.7*0.9)/(0.69) = 0.9130`

91.30% probability that they have followed the professor's study recommendation