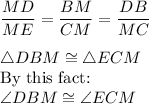Question

Given: DM⩭ME, BM⩭CM, D is the midpoint of AB, E is the midpoint of AC.
Prove: ∠DBM⩭∠ECM

Answer 1

Complete Question

In Triangle ABC

Given: DM⩭ME, BM⩭CM, D is the midpoint of AB, E is the midpoint of AC.

Prove: ∠DBM⩭∠ECM

Answer:

Proved

Explanation:

Given: DM⩭ME, BM⩭CM

Consider Triangles DBM and ECM in the diagram

`(DM)/(ME)= (BM)/(CM)\\`

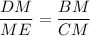
Since DB and MC are the third lengths of the two triangles with two congruent lengths, then
`DB \cong MC`

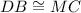
Therefore:

`(MD)/(ME)= (BM)/(CM)=(DB)/(MC)\\\\ \triangle DBM \cong \triangle ECM\\$By this fact:\\\angle DBM \cong \angle ECM`