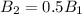Complete Question
. Two circular loops carry identical currents, but the radius of one loop is twice that of the other. How do the magnetic fields at the centers of the loops compare?
a) In both cases, the magnetic field at the center would be zero tesla.
b) The magnetic field at the center of the larger loop is twice that at the center of the smaller loop.
c) The magnetic field at the center of the larger loop is the same as that at the center of the smaller loop.
d) The magnetic field at the center of the larger loop is one-half that at the center of the smaller loop.
e) The magnetic field at the center of the larger loop is one-fourth that at the center of the smaller loop.
Answer:
The correct option is d
Step-by-step explanation:
From the question we are told that
The radius of first loop is
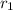
The radius of the second loop is
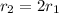
Generally magnetic field at the center of the first loop is mathematically represented as
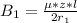
Generally magnetic field at the center of the second loop is mathematically represented as
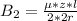
=>