Question

The biotech company Olderna has developed a new coronovirus vaccine it calls bug-b-gone or BBG. Unfortunately, it requires a fermentation process involving iguana eggs, making the marginal cost of the vaccine quite high. The cost function for doses of BBG is C(q) = 5,000 + 0.1q2 (where q is millions of doses). Demand for the vaccine in the US is projected to be D(p) = 90 - 5p, again in millions of doses. That means inverse demand, p(Q) = 18 - 0.2 Q. Part 1. Assume Oderna has a patent on the vaccine? How many (million) doses should it produce if it is maximizing profits from BBG? It should produce q = million doses. Part 2. What is the producer surplus of Olderna at the monopoly price and quantity? The PS will be million.

Answer 1

1. q = 60 million doses

2. 360 millions

Step-by-step explanation:

Given that:

The cost function C(q) = 5,000 + 0.1q²

Then, the Marginal cost MC =
`(dC)/(dq) = 0.2 \ q`

Again, inverse demand curve p(q) = 18 - 0.2 q

Then the total revenue TR =
`p*q = 18 -0.2q^2`

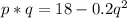
Also; the marginal revenue MR =
`(dTR)/(dq)`

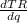
= 18 - 0.1q

In the bid to maximize profits from BBG; MR = MC

i.e

18 - 0.1 q = 0.2 q

0.3 q = 18

q = 18/0.3

q = 60 million doses

At the profit maximizing output, the price charged will be equal to :

`\mathbf{p_m = 18-(0.2*60)} \\ \\ \mathbf{p_m = 18-12} \\ \\ \mathbf{p_m = 6\ dollars \ per \ dose}`

Thus; producer surplus of Olderna at the monopoly price and quantity = price × quantity

= $6 × 60 millions

= 360 millions