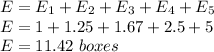Answer:
11.42 boxes
Explanation:
For the first box bought, there is a 100% chance of getting a unique toy (since you still don't have any). E₁ = 1.
After that, there is a 4 in 5 chance of getting a unique toy from the next box, the expected number of boxes required is:
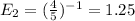
For the next unique toy, there is now a 3 in 5 chance of getting it:
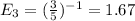
Following that logic, there is a 2 in 5 chance of getting the 4th unique toy:
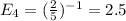
Finally, there is a 1 in 5 chance to get the last unique toy:
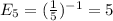
The expected number of boxes to obtain a full set is: