Question

1. Answer the following questions. (a) Check whether or not each of f1(x), f2(x) is a legitimate probability density function f1(x) = ( 0.5(3x − x3) 0< x < 2 0 otherwise f2(x) = ( 0.5(3x − x2) 0< x < 2 0 otherwise (b) Let X denote the resistance of a randomly chosen resistor, and suppose that its PDF is given by f(x) = ( kx 8  x  10 0 otherwise (i) Find k and the CDF of X, and use the CDF to calculate P(8.6  X  9.8). (ii) Find the conditional probability that X  9.8 given that X # 8.6.

Answer 1

f1 ( x ) valid pdf . f2 ( x ) is invalid pdf

k = 1 / 18 , i ) 0.6133 , ii ) 0.84792

Explanation:

Solution:-

A) The two pdfs ( f1 ( x ) and f2 ( x ) ) are given as follows:

`f_1(x) = \left \{ {{0.5(3x-x^3) } .. 0 < x < 2 \atop {0} } \right. \\\\f_2(x) = \left \{ {{0.3(3x-x^2) } .. 0 < x < 2 \atop {0} } \right. \\`

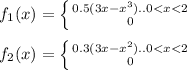
- To check the legitimacy of a continuous probability density function the area under the curve over the domain must be equal to 1. In other words the following:

`\int\limits^a_b {f_1( x )} \, dx = 1\\\\ \int\limits^a_b {f_2( x )} \, dx = 1\\`

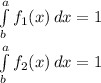
- We will perform integration of each given pdf as follows:

`\int\limits^a_b {f_1(x)} \, dx = \int\limits^2_0 {0.5(3x - x^3 )} \, dx \\\\\int\limits^a_b {f_1(x)} \, dx = [ 0.75x^2 - 0.125x^4 ]\limits^2_0\\\\\int\limits^a_b {f_1(x)} \, dx = [ 0.75*(4) - 0.125*(16) ]\\\\\int\limits^a_b {f_1(x)} \, dx = [ 3 - 2 ] = 1\\`

`\int\limits^a_b {f_2(x)} \, dx = \int\limits^2_0 {0.5(3x - x^2 )} \, dx \\\\\int\limits^a_b {f_1(x)} \, dx = [ 0.75x^2 - (x^3)/(6) ]\limits^2_0\\\\\int\limits^a_b {f_1(x)} \, dx = [ 0.75*(4) - ((8))/(6) ]\\\\\int\limits^a_b {f_1(x)} \, dx = [ 3 - 1.3333 ] = 1.67 \\eq 1 \\`

Answer: f1 ( x ) is a valid pdf; however, f2 ( x ) is not a valid pdf.

B)

- A random variable ( X ) denotes the resistance of a randomly chosen resistor, and the pdf is given as follows:

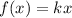`f ( x ) = kx` if 8 ≤ x ≤ 10

0 otherwise.

- To determine the value of ( k ) we will impose the condition of validity of a probability function as follows:

`\int\limits^a_b {f(x)} \, dx = 1\\`

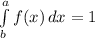
- Evaluate the integral as follows:

`\int\limits^1_8 {kx} \, dx = 1\\\\(kx^2)/(2) ]\limits^1^0_8 = 1\\\\k* [ 10^2 - 8^2 ] = 2\\\\k = (2)/(36) = (1)/(18)`... Answer

- To determine the CDF of the given probability distribution we will integrate the pdf from the initial point ( 8 ) to a respective value ( x ) as follows:

`cdf = F ( x ) = \int\limits^x_8 {f(x)} \, dx\\\\F ( x ) = \int\limits^x_8 {(x)/(18) } \, dx\\\\ F ( x ) = [ (x^2)/(36) ] \limits^x_8\\\\F ( x ) = (x^2 - 64)/(36)`

To determine the probability p ( 8.6 ≤ x ≤ 9.8 ) we will utilize the cdf as follows:

p ( 8.6 ≤ x ≤ 9.8 ) = F ( 9.8 ) - F ( 8.6 )

p ( 8.6 ≤ x ≤ 9.8 ) =
`((9.8)^2 - 64)/(36) - ((8.6)^2 - 64)/(36) = 0.61333`

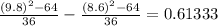
ii) To determine the conditional probability we will utilize the basic formula as follows:

p ( x ≤ 9.8 | x ≥ 8.6 ) = p ( 8.6 ≤ x ≤ 9.8 ) / p ( x ≥ 8.6 )

p ( x ≤ 9.8 | x ≥ 8.6 ) = 0.61333 / [ 1 - p ( x ≤ 8.6 ) ]

p ( x ≤ 9.8 | x ≥ 8.6 ) = 0.61333 / [ 1 - 0.27666 ]

p ( x ≤ 9.8 | x ≥ 8.6 ) = 0.61333 / [ 0.72333 ]

p ( x ≤ 9.8 | x ≥ 8.6 ) = 0.84792 ... answer