Let's check one by one
#1
And
- A$\subset$ (B U C)
- A$\subset$ B U A$\subset$ C
Till now it's ok but
- (A UB)$\cap$ C
- A$\cap$ C U B$\cap$C
But as B$\cap$ C has no elements this expression yields A$\cap$ C
Hence
#2
Solve RHS
- (A UC )$\cap$ B
- A$\cap$ B U B$\cap$ C
But according to first statement second part has no elements so it yields only
And
It denotes to common elements of A and B not all elements of A
Hence
#3
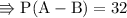
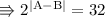
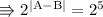
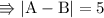
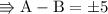
As elements can't be negative integer it's only 5.
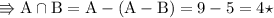
And
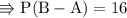
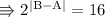
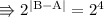
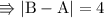
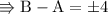
Again take it positive 4
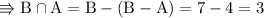
As
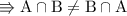
Conclusion:-
All statements are incorrect