Question

g In the western region of the state the times of all boys running in this event are normally distributed with standard deviation 12 seconds, but with mean 5 minutes 22 seconds. Find the proportion of boys from this region who qualify to run in this event in the state

Answer 1

Complete Question

The average finishing time among all high school boys in a particular track event in a certain state is 5 minutes 17 seconds. Times are normally distributed with standard deviation 12 seconds.

a. The qualifying time in this event for participation in the state meet is to be set so that only the fastest 5% of all runners qualify. Find the qualifying time in seconds (round it to the closest second). (Hint: Convert minutes to seconds.)

b. In the western region of the state the times of all boys running in this event are normally distributed with standard deviation 12 seconds, but with mean 5 minutes 22 seconds. Find the proportion of boys from this region who qualify to run in this event in the state meet. (Hint: normalcdf)

Answer:

a

The qualifying time is
`P(0.05) = 297 \sec`

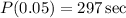
b

The proportion of boy that qualify id 0.0197 of all the boys from west region that participated in the event

Explanation:

Considering a

The mean is
`\mu_t = 5min 17 sec = 317 sec`\

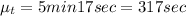The standard deviation is
`\sigma = 12 \ sec`

The percentage of success is 5% =0.05

Now since the times is normally distributed the critical value of success obtained from the standardized normal distribution table is

`t_(0.05) = -1.645`

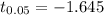
So the qualifying time is mathematically represented as

`P(t) = (\mu_t + t_(0.05) ) \sigma`

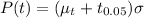
substituting values

`P(0.05) = (317 - 1645 ) *12`

`P(0.05) = 297 \sec`

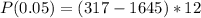
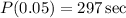
Considering b

The means is
`\mu_b = 5min22sec = 322 \ sec`

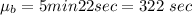
Now from a the qualifying time is
`P(0.05) = 297 \sec`

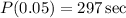
Now the proportion of boys that will qualify to run in this event in the state is area under the normal curve for

`Z = (\mu_t - \mu_b)/(\sigma )`

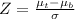
substituting values

`Z = (297.26 -322)/(12 )`

`Z = -2.06`

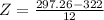
So

P(Z<=-2.06) = 0.0197