Answer:
The lest distance in feet that could have been traveled is 480 + 480·√3 feet or approximately 1311.38 feet
Explanation:
The parameters given are;
Six boys equally spaced round a circle
Radius of circle = 40 feet
Angle subtended by the arc between 2 boys = 360°/6 = 60°
Path of motion of each boy = To the other non adjacent boys = Inscribed Kite
∴ Path of motion of each boy = Right kite
Interior angles of the right kite = 90°, 90°, 120°, 60° (Angles subtended at the center = 2 × angle at the circumference)
Hence distance traveled by each boy = Perimeter of the right kite
Therefore, the distance traveled by each boy = 2 × (Long diagonal × sin((largest angle)/2) + Long diagonal × cos((largest angle)/2)
The distance traveled by each boy = 2 × (80 × sin(60) + 80 × cos(60))
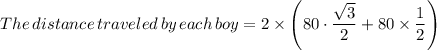

Hence we have;
The distance traveled by the six boys = 6 × (80 + 80·√3) = 480 + 480·√3 feet.
The lest distance in feet that could have been traveled = 480 + 480·√3 feet = 1311.38 feet.