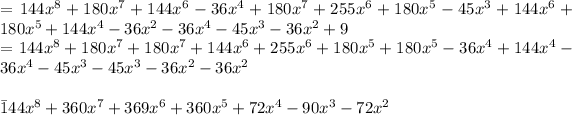Answer:
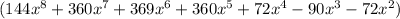
Explanation:
To better understand the question we need to properly format the expression

as we can see we have three brackets, we can proceed by first opening the first two brackets, we have.
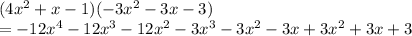
we then continue by collecting like terms

we then solve for the remaining two brackets
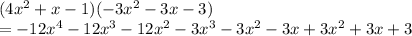
we then continue by collecting like terms

from the two brackets we obtained
 each, we now have to multiply both terms together and solve we have
each, we now have to multiply both terms together and solve we have

collecting and summing all like terms we have