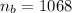Question

How's the economy? A pollster wants to construct a confidence interval for the proportion of adults who believe that economic conditions are getting better. Part: 0 / 20 of 2 Parts Complete Part 1 of 2 (a) A poll taken in July estimates this proportion to be . Using this estimate, what sample size is needed so that the confidence interval will have a margin of error of ? A sample of adults is needed to obtain a confidence interval with a margin of error of .

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

The sample size is
`n =944`

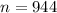
b

The sample size is
`n_b = 1068`

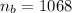
Explanation:

From the question we are told that

The proportion is mathematically represented as
`\r p = 0.33`

The marginal error is
`e = 0.03`

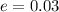
The confidence level is 95 % = 0.95

The z-value of the confidence level is

`z_c = 1.96`

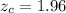
This value is obtained from the z table

The sample size is mathematically evaluated as

`n = [(z_c)/(e) ]^2 * \r p(1- \r p)`

substituting values

`n = [(1.96)/(0.03) ]^2 * 0.33 (1- 0.33)`

`n =944`

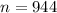
If no estimate is available the let assume
`\r p = 0.50`

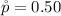
So

`n_b = [(z_c)/(e) ]^2 * \r p(1- \r p)`

substituting values

`n_b = [(1.96)/(0.03) ]^2 * 0.50 (1- 0.50)`

`n_b = 1068`