Question

An airport has two long term parking lots. the cost to park,y, in each lot for x days is shown in the tables

a system of linear equations can be used to determine on which day the cost to park is the same for both lots. one of the equations in the system is y=6x. what is the other equation in the system?

Answer 1

y = 4x + 12 will be the other equation.

Explanation:

Data given in the tables show a linear relation (has a common data).

To get the linear relation, we will choose the two points from table (1) .

Let the points are (1, 16) and (2, 20).

Slope of the line 'm' =
`\frac{\triangle{y}}{\triangle{x}}`

m =
`(20-16)/(2-1)`

m =
`(4)/(1)`

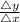
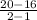
m = 4

Equation of the line passing through (1, 16) having slope = 4

y - 16 = 4(x - 1)

y = 4(x - 1) + 16

y = 4x - 4 + 16

y = 4x + 12

Now we take second set of data,

We choose two points (1, 6) and (2, 12).

Slope 'm' =
`\frac{\triangle{y}}{\triangle{x}}`

m =
`(12-6)/(2-1)`

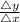
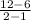
m = 6

Equation of the line passing through (1, 6) having slope = 6

y - 6 = 6(x - 1)

y = 6x - 6 + 6

y = 6x

Therefore, other equation of the system of equations will be,

y = 4x + 12