Answer:
225 students scored 65 or better and 75 students scored 88 or better.
Explanation:
We are given that The five-number summary for the scores of 300 nursing students are given :
Minimum = 40
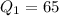
Median = 82

Maximum = 100
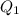 is the first quartile and is the median of the lower half of the data set. 25% of the numbers in the data set lie below
is the first quartile and is the median of the lower half of the data set. 25% of the numbers in the data set lie below
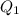 and about 75% lie above
and about 75% lie above
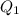 .
.
 is the third quartile and is the median of the upper half of the data set. 75% of the numbers in the data set lie below
is the third quartile and is the median of the upper half of the data set. 75% of the numbers in the data set lie below
 and about 25% lie above
and about 25% lie above

i) .About how many students scored 65 or better?
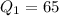
Since we know that 75% lie above
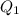 .
.
So, Number of students scored 65 or better =
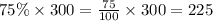
ii)About how many students scored 88 or better?

Since we know that 25% lie above

So, Number of students scored 88 or better =
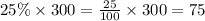
Hence 225 students scored 65 or better and 75 students scored 88 or better.