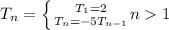Answer:
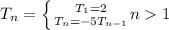
Explanation:
Given
Geometric sequence: 2, -10, 50, -250
Required
Recursive formula of the sequence
We start by naming each sequence
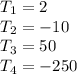
Represent each term in relation to the previous term (except T1)
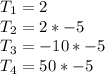
Recall that
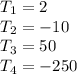
So, at this point; we have to make substitutions
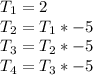
Subtract 1 from each term on the right hand side
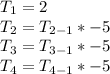
Replace each term greater than 1 by n
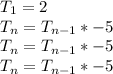
Remove repetition
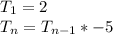
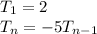
Hence, the recursive formula is