Question

On a linear X temperature scale, water freezes at −115.0°X and boils at 325.0°X. On a linear Y temperature scale, water freezes at −65.00°Y and boils at −25.00°Y. A temperature of 50.00°Y corresponds to what temperature on the X scale?

Answer 1

The current temperature on the X scale is 1150 °X.

Explanation:

Let is determine first the ratio of change in X linear temperature scale to change in Y linear temperature scale:

`r = (\Delta T_(X))/(\Delta T_(Y))`

`r = (325\,^(\circ)X-(-115\,^(\circ)X))/(-25\,^(\circ)Y - (-65.00\,^(\circ)Y))`

`r = 11\,(^(\circ)X)/(^(\circ)Y)`

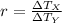
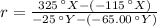
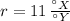
The difference between current temperature in Y linear scale with respect to freezing point is:

`\Delta T_(Y) = 50\,^(\circ)Y - (-65\,^(\circ)Y)`

`\Delta T_(Y) = 115\,^(\circ)Y`

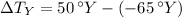
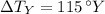
The change in X linear scale is:

`\Delta T_(X) = r\cdot \Delta T_(Y)`

`\Delta T_(X) = \left(11\,(^(\circ)X)/(^(\circ)Y) \right)\cdot (115\,^(\circ)Y)`

`\Delta T_(X) = 1265\,^(\circ)X`

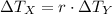
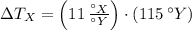
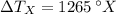
Lastly, the current temperature on the X scale is:

`T_(X) = -115\,^(\circ)X + 1265\,^(\circ)X`

`T_(X) = 1150\,^(\circ)X`

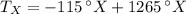
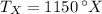
The current temperature on the X scale is 1150 °X.