Question

An unpolarized beam of light with an intensity of 8000 W/m2 is incident on two ideal polarizing sheets. If the emerging light has an intensity 0.2 times the original intensity of the incident beam, what is the angle between the two polarizers

Answer 1

50.76°

Step-by-step explanation:

To find the angle between the two polarizers, you take into account that each polarizing sheet reduces the intensity of the light. Then, you have:

After the unpolarized light crosses the first polarizer:

`I_1=(I_o)/(2)`

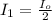
After light crosses the second polarizer:

`I_2=I_1cos^2\theta=(I_o)/(2)cos^2\theta`

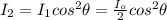
θ: angle between the two polarizing sheets

When the light emerges from the second polarizer the intensity of the light is 0.2 times the initial intensity, then you have:

`0.2(8000W/m^2)=((8000Wm/m^2)/(2))cos^2(\theta)\\\\\theta=cos^(-1)(√(0.4))=50.76\°`

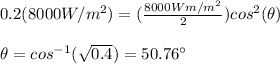
hence, the angle between the polarizing sheets is 50.76°