Question

A circular radar antenna on a Coast Guard ship has a diameter of 2.10 m and radiates at a frequency of 16.0 GHz. Two small boats are located 7.00 km away from the ship. How close together could the boats be and still be detected as two objects

Answer 1

d = 76.5 m

Step-by-step explanation:

To find the distance at which the boats will be detected as two objects, we need to use the following equation:

`\theta = (1.22 \lambda)/(D) = (d)/(L)`

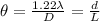
Where:

θ: is the angle of resolution of a circular aperture

λ: is the wavelength

D: is the diameter of the antenna = 2.10 m

d: is the separation of the two boats = ?

L: is the distance of the two boats from the ship = 7.00 km = 7000 m

To find λ we can use the following equation:

`\lambda = (c)/(f)`

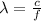
Where:

c: is the speed of light = 3.00x10⁸ m/s

f: is the frequency = 16.0 GHz = 16.0x10⁹ Hz

`\lambda = (c)/(f) = (3.00 \cdot 10^(8) m/s)/(16.0 \cdot 10^(9) s^(-1)) = 0.0188 m`

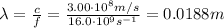
Hence, the distance is:

`d = (1.22 \lambda L)/(D) = (1.22*0.0188 m*7000 m)/(2.10 m) = 76.5 m`

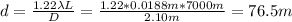
Therefore, the boats could be at 76.5 m close together to be detected as two objects.

I hope it helps you!