Question

Given the polynomial f(x)=x3+x2+ax−9 and the fact that (x−3) is a factor of the polynomial, what is the value of a?

Answer 1

`a = -9`.

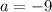Explanation:

Let
`b` be a real number. Consider the factor theorem: if
`(x - b)` is a factor of the function
`f(x)`, then it must be true that
`f(b) = 0`.

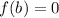To solve this question, assume that
`a` has already been found. Since
`(x - 3)` is a factor of this polynomial,
`f(3) = 0` by the factor theorem.

The left-hand side of this equation can be expressed as:

`\begin{aligned}f(3) &= 3^3 + 3^2 + 3\, a - 9 = 27 + 3\, a\end{aligned}`.

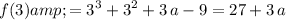That should match the
`0` on the right-hand side. In other words:

`27 + 3\, a= 0`.

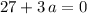Solve for
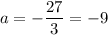`a`:

`\displaystyle a = -(27)/(3) = -9`.