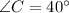Question

Given: ΔABC

m∠1=m∠2
D∈
AC
, BD = DC
m∠BDC = 100°
Find: m∠A, m∠B, m∠C

Answer 1

`\angle A = 60^(\circ)` ,
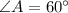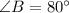`\angle B = 80^(\circ)`and
`\angle C = 40^(\circ)`

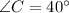
Explanation:

We are given that BD = DC

BD= DC

So,
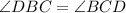`\angle DBC = \angle BCD` (Opposite angles of equal sides are equal) ----1

We are given that ∠BDC = 100°

In ΔBDC

Angle sum property of triangle : The sum of all angles of triangle is 180°

So,
`\angle BDC+\angle DBC +\angle BCD = 180^(\circ)`

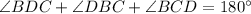
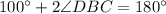`100^(\circ)+2 \angle DBC= 180^(\circ)`(Using 1)

`2 \angle DBC = 180^(\circ)-100^(\circ)`

`2 \angle DBC = 80^(\circ)`

`\angle DBC = 40^(\circ)`

`\angle DBC = \angle BCD=\angle 2 = 40^(\circ)`

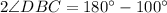
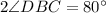
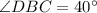
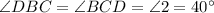
So,
`\angle C = 40^(\circ)`

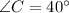
We are given that
`\angle 1 = \angle 2`

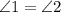
So,
`\angle 1 = \angle 2 = 40^(\circ)`

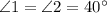
Now
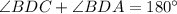`\angle BDC+\angle BDA = 180^(\circ)`(Linear pair)

`100^(\circ)+\angle BDA = 180^(\circ)\\\angle BDA =80^(\circ)`

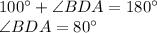
In ΔABD

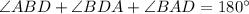`\angle ABD+\angle BDA+\angle BAD = 180^(\circ)`(Angle sum property)

`\angle 1 +\angle BDA+\angle BAD = 180^(\circ)\\40^(\circ)+80^(\circ)+\angle BAD = 180^(\circ)\\120^(\circ)+\angle BAD = 180^(\circ)\\\angle BAD =60^(\circ)`

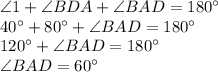
So,
`\angle A =60^(\circ)\\\angle B = \angle 1+\angle 2 = 40^(\circ)+40^(\circ)=80^(\circ)`

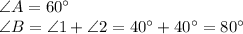
Hence
`\angle A = 60^(\circ)` ,
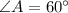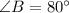`\angle B = 80^(\circ)`and
`\angle C = 40^(\circ)`