Answer:
The random two-sided 95% confidence interval estimator for p is
(0.5192 , 0.5807)
Explanation:
step(i):-
Given toss the coin 1000 times to find 550 of them were heads
given sample size n =1000
x = 550
sample proportion
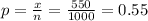

Step(ii):-
The random two-sided 95% confidence interval estimator for p is determined by
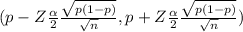
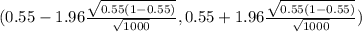
(0.55 - 1.96 X 0.0157 , 0.55 + 1.96 X 0.0157)
(0.5192 , 0.5807)
conclusion:-
The random two-sided 95% confidence interval estimator for p is
(0.5192 , 0.5807)
confidence interval say the Population of proportion is lies between in these interval.