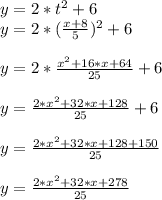Answer:
The rectangular form is:
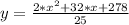
Explanation:
In order to write the rectangular form we need to find the value of "t" in relation to "x", which means isolating the "t" variable on the left side of the second equation, following that we will use that value of "t" on the first one as shown below:
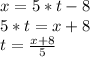
Applying on the first equation: