Question

Find two consecutive positive integers such that the square of the first decreased by 67 is equal to three times the second

Answer 1

The numbers are 10 and 11.

Explanation:

Let
`x` and
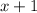`x+1` be consecutive positive integers.

When the problem says that the square of the first decreased by 67 this means
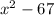`x^2-67` and this is equal to three times the second
`3(x+1)`.

So
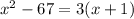`x^2-67=3(x+1)` will be our equation.

Next, we solve the equation:

`x^2-67=3x+3\\\\x^2-70=3x\\\\x^2-3x-70=0`

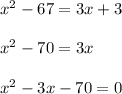
Solve by factoring

`x^2-3x-70= \left(x^2+7x\right)+\left(-10x-70\right)\\\\x^2-3x-70=x\left(x+7\right)-10\left(x+7\right)\\\\x^2-3x-70=\left(x+7\right)\left(x-10\right)=0`

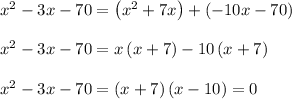
Using the Zero Factor Principle: If ab = 0, then either a = 0 or b = 0, or both a and b are 0.

`x+7=0\\x=-7`

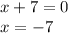
And

`x-10=0\\x=10`

Because the numbers need to be positive integers, we only take x = 10 as a valid solution.

The numbers are 10 and 11.