Question

California is 0.5 minutes. To investigate the validity of this claim a random sample of 6 earthquakes were taken and the sample mean and the sample standard deviation were 1.15 and 0.308 and minutes, respectively. Construct a 98% confidence interval and determine if the researcher`s claim can be rejected. g

Answer 1

98% confidence interval for the mean is

(0.72689 , 1.57311)

Explanation:

Given random sample size 'n' = 6

Given sample mean x⁻ = 1.15

Given sample standard deviation 'S' = 0.308

98% confidence interval for the mean is determined by

`(x^(-) - t_{(\alpha )/(2) } (S)/(√(n) ) , x^(-) + t_{(\alpha )/(2) } (S)/(√(n) ) )`

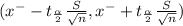
Degrees of freedom ν =n-1 =6-1 =5

Critical value : -

`t_{(0.02)/(2) } = t_(0.01) = 3.365`

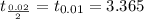
98% confidence interval for the mean is determined by

`(1.15 - 3.365(0.308)/(√(6) ) , 1.15+ 3.365(0.308)/(√(6) ) )`

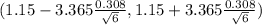
On calculation , we get

( 1.15 - 0.42311 , 1.15+ 0.42311)

(0.72689 , 1.57311)

Final answer:-

98% confidence interval for the mean is

(0.72689 , 1.57311)