Answer:
98% confidence interval for the mean is
(0.72689 , 1.57311)
Explanation:
Given random sample size 'n' = 6
Given sample mean x⁻ = 1.15
Given sample standard deviation 'S' = 0.308
98% confidence interval for the mean is determined by
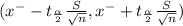
Degrees of freedom ν =n-1 =6-1 =5
Critical value : -
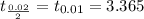
98% confidence interval for the mean is determined by
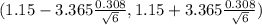
On calculation , we get
( 1.15 - 0.42311 , 1.15+ 0.42311)
(0.72689 , 1.57311)
Final answer:-
98% confidence interval for the mean is
(0.72689 , 1.57311)