Answer:
14.20669 years
Roughly 14 years and 2.5 months.
Explanation:
Assuming this is compound interest.
The formula is

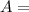 Final Amount
Final Amount
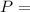 Principal Amount
Principal Amount
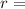 Interest Rate
Interest Rate
 # of times interest is compounded per year
# of times interest is compounded per year
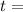 Time in years
Time in years
We are looking for the times in years to double the money so
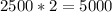
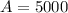

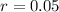
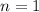
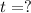
Lets solve for
 .
.
Step 1.
Plug in our numbers into the compound interest formula.
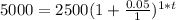
Step 2.
Simplify the equation.
Evaluate
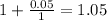
Evaluate
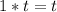
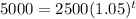
Step 3.
Divide both sides of the equation by
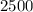
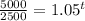
Evaluate
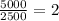
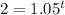
Step 4.
Take the natural log of both sides of the equation and rewrite the right side of the eqaution using properties of exponents/logarithms.
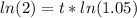
Step 5.
Divide both sides of the equation by
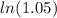
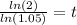
Step 6.
Evaluate
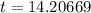
Roughly 14 years and 2.5 months.