Question

According to the Rational Root Theorem, which number is a potential root of f(x) = 9x8 + 9x6 – 12x + 7?

Answer 1

its D, 3/7.

Explanation:

just did it egen2020

Answer 2

`\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)`.

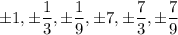Explanation:

According to the Rational Root Theorem, the potential roots of a polynomial are

`x=\pm(p)/(q)`

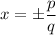
where, p is a factor of constant and q is a factor of leading term.

The given polynomial is

`f(x)=9x^8+9x^6-12x+7`

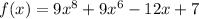
Here, 9 is the leading term and 7 is constant.

Factors of 9 are ±1, ±3, ±9.

Factors of 7 are ±1, ±7.

Using rational root theorem, the rational or potential roots are

`x=\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)`

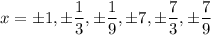
Therefore, the potential root of f(x) are
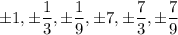`\pm 1, \pm(1)/(3),\pm(1)/(9),\pm 7, \pm(7)/(3),\pm(7)/(9)`.