1 Answer

Maxtuzz · Answer 1 · 2021-12-29T00:32:02+0000

The Options are:

Answer:

(B) (5x-8y)(5x+8y)

Explanation:

Given the binomial:
25x^2-64y^2

$25x^2-64y^2\\=5^2x^2-8^2y^2\\=(5x)^2-(8y)^2$

The essence of expressing it in this form is so as to be able to apply a principle of factorization called the "Difference of Two Squares"

Difference of Two Squares:
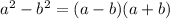
a^2-b^2=(a-b)(a+b)

Therefore taking: a=5x; b=8y

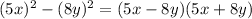
$(5x)^2-(8y)^2=(5x-8y)(5x+8y)\\$

Thus (5x-8y)(5x+8y) is the factorization of the binomial
25x^2-64y^2 .

The correct option is B

Please log in or register to add a comment.