Answer:
a) About 99.7% of the organs will be within 245 and 455 grams.
b) 95% weighs between 280 grams and 420 grams.
c) 5% of the organs weighs less than 280 grams or more than 420 grams
d) 68% weighs between 245 grams and 385 grams.
Explanation:
The empirical rule tells us that is expected to have 68% of the data within 1 standard deviation from the mean, 95% in the interval of 2 standard deviations and 99.7% in the interval of 3 standard deviations.
In this case, the mean is 350 grams and the standard deviation is 35 grams.
a) This corresponds to ±3 standard deviations.
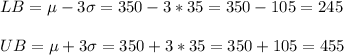
b) We have to calculate how many standard deviations correspond to this interval.
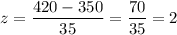
For 2 standard deviations, 95% of the data willl fall within the interval.
c) As 95% lies within 240 and 420 grams, then 1-0.95=0.05=5% lies outside this bounds.
d) We have to calculate how many standard deviations correspond to this interval.
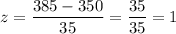
For 1 standard deviations, 68% of the data willl fall within the interval.