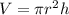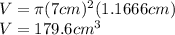Answer:
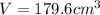
Explanation:
the volume of a cylinder is given by:
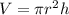
where r is the radius and h is the height.
and the surface area:
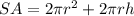
the first term is the area of the circles and the second term is the area of the body.
since "The number of volume of a cylinder is half of its number of the total surface area." we will have that:
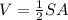
substitutig the equivalent expressions on each side:
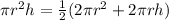
and we simplify and solve for the height (since is the value we don't know of the cylinder):
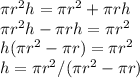
we substitute the value of the radius
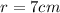 , and we get:
, and we get:
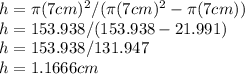
thus the volume is: