Question

The triangular pyramid shown is made up of four congruent triangles. The length of the base is 8 inches, and the height of the base is 6.9 inches. A triangular pyramid. Talia is finding the lateral area of the pyramid. She says that the expression 4 (one-half (8) (6.9)) represents the lateral area. Which explains whether Talia is correct and why? Talia is correct. The three faces have the same area as the base, and the area of the base is One-half (8) (6.9). Talia is correct. The lateral area can be found by approximating one large triangle, which can be found using the expression 4 (one-half (8) (6.9)). Talia is not correct. Only the base has an area of One-half (8) (6.9), and three other faces have a different area. Talia is not correct. The lateral area has three faces, so the expression should be 3 (one-half (8) (6.9)).

Answer 1

(B) Talia is correct. The lateral area can be found by approximating one large triangle, which can be found using the expression 4 (one-half (8) (6.9))

Explanation:

Base of the Pyramid = 8 Inches

Height of the Triangular Face = 6.9 Inches

In any solid shape, the Lateral surface area is the sum of all sides except its top and bottom bases.

Since the four triangles are congruent:

Lateral Surface Area = 4 X Area of One Triangle

Area of a Triangle =
`(1)/(2)$ X Base X Height`

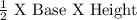
Area of one Triangular Face
`= (1)/(2)(8)(6.9)`

Therefore:

Lateral Surface Area
`= 4\left((1)/(2)(8)(6.9)\right)`

Therefore, Talia is correct.