Answer:
Explanation:
Given a function f, whose derivatives are f' and f'', a value x is a critical point if f'(x) =0. A value x is a minimum of f if it is a critical point and f''(x) >0 and it is maximum if f''(x)<0. We will perfom the following steps:
1. Calculate the derivative f'.
2. Solve f'(x) =0.
3. Determine if the x value found in 2 is a minimum or a maximum using f''.
Recall the following properties of derivatives
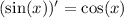
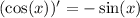
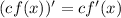 where c is a constant.
where c is a constant.
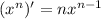
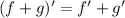 where f,g are differentiable.
where f,g are differentiable.
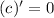 where c is a constant.
where c is a constant.
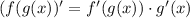 (chain rule)
(chain rule)
Case 1: f(x) = 2+3x+3.
Using the properties from above, we have
1.
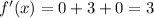
2. The equation f'(x)=0 where f'(x) = 3 has no solution.
3. Based on the previous result, f has no maximum nor minimum.
Case 2:

1.
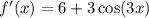
2. We have the equation
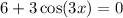
which is equivalent to

Recall that the cosine function only takes values in the set [-1,1]. So, this equation has no solution.
3. Based on the previous result, f has no maximum nor minimum.