Question

f the price charged for a candy bar is​ p(x) cents, where p (x )equals 162 minus StartFraction x Over 10 EndFraction ​, then x thousand candy bars will be sold in a certain city.

Answer 1

a)
`R(x) = 162,000x-100x^2`

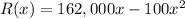
b) x = 810

c) 656,100$

Explanation:

`p(x) = 162- (x)/(10)`

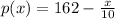
a) find expression for total revenue from sale ox x thousand candy bars

R(x) = (x)[p(x)]

R(x) = x(162 - x/10)

therefore,
`R(x) = 162,000x-100x^2`

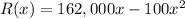
b) find value of x that leads to maximum revenue

take derivative of R(x), which is:
`R'(x) = 162,000-200x`

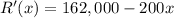
set that equation equal to 0 and solve for critical number(s):
`162,000-200x=0`

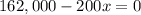
therfore, critical number is: x = 810

**this critical number is the x-value that leads to max. revenue

c) find the maximum revenue

take original R(x) formula, and insert the critical number you just solved for and insert it into there to solve for part c.

`R(x) = 162,000x-100x^2`

`R(810)=162,000(810)-100(810)^2`

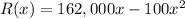
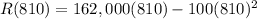
therefore, your maximum revenue in dollars is: 656,100$

Answer 2

a. 1620-x^2

b. x=810

c. Maximum value revenue=$656,100

Explanation:

(a) Total revenue from sale of x thousand candy bars

P(x)=162 - x/10

Price of a candy bar=p(x)/100 in dollars

1000 candy bars will be sold for

=1000×p(x)/100

=10*p(x)

x thousand candy bars will be

Revenue=price × quantity

=10p(x)*x

=10(162-x/10) * x

=10( 1620-x/10) * x

=1620-x * x

=1620x-x^2

R(x)=1620x-x^2

(b) Value of x that leads to maximum revenue

R(x)=1620x-x^2

R'(x)=1620-2x

If R'(x)=0

Then,

1620-2x=0

1620=2x

Divide both sides by 2

810=x

x=810

(C) find the maximum revenue

R(x)=1620x-x^2

R(810)=1620x-x^2

=1620(810)-810^2

=1,312,200-656,100

=$656,100