Question

An insurance company issues 1250 vision care insurance policies. The number of claims filed by a policyholder under a vision care insurance policy during one year is a Poisson random variable with mean 2. Assume the numbers of claims filed by different policyholders are mutually independent. Calculate the approximate probability that there is a total of between 2450 and 2600 claims during a one-year period?

Answer 1

Explanation:

The total number of claim is the sum S of 1250 independent random variables,

each having poisson distribution with mean μ = 2

Since the Variance of poisson distribution is equal to its mean ,

the standard deviation of this is

`\sigma= √(2)`

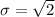
By the CLT is follow that S is approximately normal with mean 1250*2 =2500

and standard deviation
`√(1250) *√(2) =50`

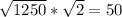
Hence, the probability to compute is

`P(2350\leq S\leq 2600)=P((2450-2500)/(50) \leq (S-2500)/(50) \leq (2600-2500)/(50) )\\\\=P(-1<2<2)\\\\=P(2\leq 2)-P(2\leq 1)\\\\=0.977249868-0.15365525\\\\=0.818594614\\\\=0.82`