Question

There are approximately 7.7 billion humans on Earth. If the virus spreads beyond the 200-person town, how long will it be until everyone on the planet is infected if the number of infected people doubles every week?

Answer 1

25.2 weeks until everyone on the planet is infected

Explanation:

The number of infected people after t weeks has the following format:

`P(t) = P(0)(1+r)^(t)`

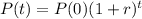
In which P(0) is the initial number of infected people and r is the growth rate, as a decimal.

The number of infected people doubles every week

This means that
`P(1) = 2P(0)`

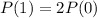
So

`P(t) = P(0)(1+r)^(t)`

`2P(0) = P(0)(1+r)`

`1 + r = 2`

`r = 1`

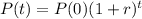
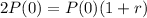
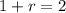
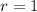
So

`P(t) = P(0)*(2)^(t)`

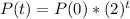
200-person town

This means that
`P(0) = 200`

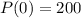
So

`P(t) = P(0)*(2)^(t)`

`P(t) = 200*(2)^(t)`

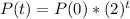
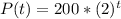
How long will it be until everyone on the planet is infected?

This is t for which P(t) = 7700000000[/tex]

So

`P(t) = 200*(2)^(t)`

`7700000000 = 200*(2)^(t)`

`2^(t) = (7700000000)/(200)`

`\log{2^(t)} = \log{(7700000000)/(200)}`

`t\log{2} = \log{(7700000000)/(200)}`

`t = \frac{\log{(7700000000)/(200)}}{\log{2}}`

`t = 25.2`

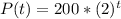
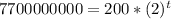
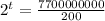
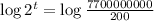
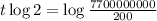
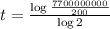
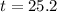
25.2 weeks until everyone on the planet is infected