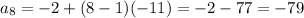Question

Find the indicated sum of each sequence S8 of -2,-13,-24,-35

Answer 1

The sum of the arithmetic sequence is
`S_(8)=-324`.

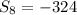Explanation:

A sequence is a set of numbers that are in order.

In an arithmetic sequence the difference between one term and the next is a constant. In other words, we just add the same value each time infinitely.

If the first term of an arithmetic sequence is
`a_1` and the common difference is d, then the nth term of the sequence is given by:

`a_(n)=a_(1)+(n-1)d`

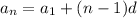
For the sequence

`-2,-13,-24,-35,...`

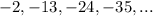
The pattern is continued by adding -11 to the last number each time.

An arithmetic series is the sum of an arithmetic sequence. We find the sum by adding the first,
`a_1` and last term,
`a_n`, divide by 2 in order to get the mean of the two values and then multiply by the number of values, n

`S_(n)=(n)/(2)(a_(1)+a_(n))`

The sum of the arithmetic sequence is

`a_(8)=-2+(8-1)(-11)=-2-77=-79`

`S_(8)=(8)/(2)(-2-79})=4\left(-2-79\right)=4\left(-81\right)=-324`