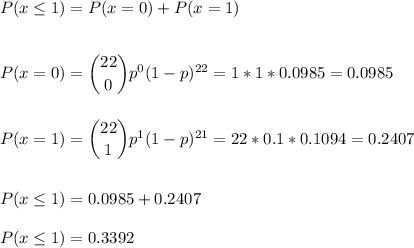Question

A firm maintains 22 cars for business purposes. From past experience, it is known that approximately 10% will require major engine service during a one-year period. What is the probability that at most 1 car will require major engine repair next year?

Answer 1

The probability that at most 1 car will require major engine repair next year is P=0.3392.

Explanation:

This can be modeled as a binomial random variable, with n=22 and p=0.1.

The probability that exavtly k cars will require major engine repair next year is:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)`

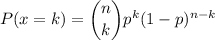
Then, the probability that at most 1 car will require major engine repair next year is:

`P(x\leq1)=P(x=0)+P(x=1)\\\\\\P(x=0) = \dbinom{22}{0} p^(0)(1-p)^(22)=1*1*0.0985=0.0985\\\\\\P(x=1) = \dbinom{22}{1} p^(1)(1-p)^(21)=22*0.1*0.1094=0.2407\\\\\\P(x\leq1)=0.0985+0.2407\\\\P(x\leq1)=0.3392`