Question

for the given license plate configuration, determine how many different plates are possinle if letters and digits (a) can ba repeated (b) can not be repeated. 3 letters followed by 2 digits

Answer 1

a) 1,757,600 different plates possible.

b) 1,404,000 different plates possible.

Explanation:

The permutations formula is important to solve this question.

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

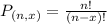
(a) can be repeated:

There are 3 letters, each one with 26 possible outcomes.

2 digits, each with 10 possible outcomes

So

T = 26*26*26*10*10 = 1757600

1,757,600 different plates possible.

(b) cannot be repeated:

Here the permutations formula is used.

Three letters, from a set of 26.

Two digits, from a set of 10. So

`T = P_((26,3))*P_((10,2)) = (26!)/((26-3)!)*(10!)/((10-2)!) = 1404000`

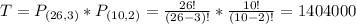
1,404,000 different plates possible.