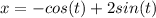Question

x = c1 cos(t) + c2 sin(t) is a two-parameter family of solutions of the second-order DE x'' + x = 0. Find a solution of the second-order IVP consisting of this differential equation and the given initial conditions. x(0) = −1, x'(0) = 2

Answer 1

`x=-cos(t)+2sin(t)`

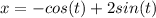
Explanation:

The problem is very simple, since they give us the solution from the start. However I will show you how they came to that solution:

A differential equation of the form:

`a_n y^n +a_n_-_1y^(n-1)+...+a_1y'+a_oy=0`

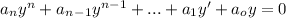
Will have a characteristic equation of the form:

`a_n r^n +a_n_-_1r^(n-1)+...+a_1r+a_o=0`

Where solutions
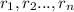`r_1,r_2...,r_n` are the roots from which the general solution can be found.

For real roots the solution is given by:

`y(t)=c_1e^(r_1t) +c_2e^(r_2t)`

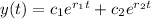
For real repeated roots the solution is given by:

`y(t)=c_1e^(rt) +c_2te^(rt)`

For complex roots the solution is given by:

`y(t)=c_1e^(\lambda t) cos(\mu t)+c_2e^(\lambda t) sin(\mu t)`

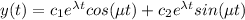
Where:

`r_1_,_2=\lambda \pm \mu i`

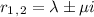
Let's find the solution for
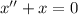`x''+x=0` using the previous information:

The characteristic equation is:

`r^(2) +1=0`

So, the roots are given by:

`r_1_,_2=0\pm √(-1) =\pm i`

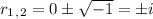
Therefore, the solution is:

`x(t)=c_1cos(t)+c_2sin(t)`

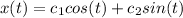
As you can see, is the same solution provided by the problem.

Moving on, let's find the derivative of
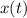`x(t)` in order to find the constants
`c_1` and
`c_2`:

`x'(t)=-c_1sin(t)+c_2cos(t)`

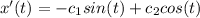
Evaluating the initial conditions:

`x(0)=-1\\\\-1=c_1cos(0)+c_2sin(0)\\\\-1=c_1`

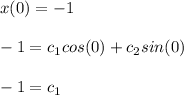
And

`x'(0)=2\\\\2=-c_1sin(0)+c_2cos(0)\\\\2=c_2`

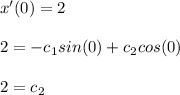
Now we have found the value of the constants, the solution of the second-order IVP is:

`x=-cos(t)+2sin(t)`