Question

The average finishing time among all high school boys in a particular track event in a certain state is 5 minutes 17 seconds. Times are normally distributed with standard deviation 12 seconds. The qualifying time in this event for participation in the state meet is to be set so that only the fastest 5% of all runners qualify. Find the qualifying time in seconds (round it to the closest second). (Hint: Convert minutes to seconds.) In the western region of the state the times of all boys running in this event are normally distributed with standard deviation 12 seconds, but with mean 5 minutes 22 seconds. Find the proportion of boys from this region who qualify to run in this event in the state meet. (Hint: normalcdf)

Answer 1

a. The qualifying time in seconds is approximately 297 sec.

b. The proportion of boys from the western region who qualify to run in this event is about 1.88% (0.0188).

Step-by-step explanation:

Part a

In this question, the key concept to take into account is the normal distribution. This distribution is completely characterized when we have the population's mean,
`\\ \mu`, and the population standard deviation,
`\\ \sigma`.

In this case:

`\\ \mu = 5\;min\;17\;sec`

`\\ \sigma = 12\;sec`

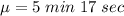
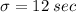
Because we are asked to finding the qualifying time in seconds, let us to convert
`\\ \mu` from minutes to seconds:

`\\ 5\;min*(60\;sec)/(1\;min)`

`\\ 5 * 60 \;sec*(min)/(min)`

`\\ 300 \;sec*1`

`\\ 300 \;sec`

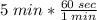
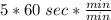
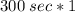
We still need to sum 17 sec:

Then,
`\\ \mu = (300 + 17)\;sec`

`\\ \mu = 317\;sec`

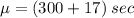
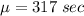
Time in seconds of the fastest 5% runners

They are those that in the normal distribution are below 5% (0.05) in the cumulative normal distribution, that is,
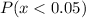`\\ P(x<0.05)`. Those above it, spend more time in the track event.

For this cumulative value, we can use the standardized score, or z-score, for solving the value in seconds that corresponds to it. The formula for the z-score is

`\\ z = (x - \mu)/(\sigma)` [1]

Where x is the raw value or, in this case, the time in seconds in question. Then, for a cumulative probability of 5%, the corresponding z-score is (consulting a cumulative normal standard table, available on the Internet or in any Statistic book):

`\\ z \approx -1.65`

For this, we need to find a cumulative probability in the cumulative standard normal table equal or approximately to 0.05, and this value is about z = -1.65.

With this value at hand, we can solve [1] for x.

`\\ z = (x - \mu)/(\sigma)`

`\\ -1.65 = (x - 317\;sec)/(12\;sec)`

`\\ -1.65 * 12\;sec = x - 317\;sec`

`\\ (-1.65 * 12\;sec) + 317\;sec = x`

`\\ -19.80\;sec + 317\;sec = x`

`\\ x = -19.80\;sec + 317\;sec`

`\\ x = 297.20\;sec`

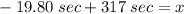
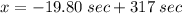
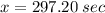
Thus, rounding it to the nearest second, we have that "the qualifying time in seconds" is, approximately, 297 sec. This is the time that the 5% fastest high school boys have to meet the state competition requirement. They spend less time to run the same distance than others.

Part b

In this part, we have to take into account the previously obtained time (297 sec) to find "the proportion of boys from this region who qualify to run in this event in the state meet." In other words, how many, in percent, can qualify, knowing that, in this part of the state (western region), the population's mean is different (5min 22sec or 300sec + 22sec = 322sec, considering that we already have the value in seconds for 5min from the previous answer).

Then, for this region, the proportion of boys that can qualify to run in this event in the state meet can be calculated using the formula [1] for z-scores:

`\\ z = (x - \mu)/(\sigma)`

Where, in this case, the value for x = 297 sec, for the reasons already explained. With the resulting value for z, we can consult the cumulative standard normal distribution to find the probability in question. Then

`\\ z = ((297 - 322)\;sec)/(12\;sec)`

`\\ z = (-25\;sec)/(12\;sec)`

`\\ z = -2.08333... \approx -2.08`

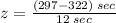
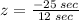
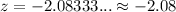
For a z = -2.08, the corresponding probability, consulting a cumulative standard normal distribution is, approximately, 0.0188 or about 1.88% of the boys for western region of the state.

Then, in other words, "the proportion of boys from this region who qualify to run in this event in the state meet" is about 1.88%.

We can see the results in the graphs below. The first graph is for western region.